
Mesurer la rotation différentielle solaire avec JSol’Ex
05 February 2026
Tags: solex jsolex solaire astronomie doppler rotation
Une boule de plasma en rotation
L’un des aspects fascinants du Soleil est qu’il ne tourne pas comme un corps solide. Contrairement à la Terre, qui effectue une rotation en 24 heures quelle que soit la latitude, la vitesse de rotation du Soleil varie avec la latitude : l’équateur tourne plus vite que les pôles. Ce phénomène, appelé rotation différentielle, est étudié depuis le 19ème siècle et reste un sujet de recherche important en physique solaire.
Les régions équatoriales du Soleil effectuent une rotation en environ 25 jours, tandis que près des pôles, cela prend environ 35 jours. Cette rotation différentielle joue un rôle clé dans le mécanisme de dynamo solaire qui génère le champ magnétique du Soleil et pilote le cycle solaire de 11 ans.

Dans cet article, je vais expliquer comment j’ai ajouté une fonctionnalité dans JSol’Ex 4.5.0 qui permet aux astronomes amateurs de mesurer cette rotation différentielle directement à partir d’un scan obtenu avec un spectrohéliographe. Une erreur fréquente est de penser que cette mesure n’est pas possible parce que la dispersion spectrale d’un spectrographe comme le Sol’Ex est typiquement d’environ 0.1 à 0.2 Å, c’est-à-dire plus grand que l’échelle de ce que nous essayons de mesurer (2 km/s, soit environ 0.04 Å). En pratique, nous devrons obtenir une précision sub-pixellaire et cet article explique comment y arriver.
L’effet Doppler
Le principe derrière la mesure est simple : l'effet Doppler. Quand une source lumineuse se déplace vers nous, la longueur d’onde est décalée vers le bleu du spectre (blueshift). Quand elle s’éloigne, la longueur d’onde se décale vers le rouge (redshift).
Puisque le Soleil tourne, un limbe se déplace toujours vers nous (le limbe Est) tandis que l’autre s’éloigne (le limbe Ouest). En mesurant le décalage de longueur d’onde d’une raie spectrale aux deux limbes, nous pouvons calculer la vitesse de rotation.

On pourrait se demander ce qu’il en est du mouvement propre de la Terre : nous orbitons autour du Soleil à environ 30 km/s, ce qui est bien plus grand que la vitesse de rotation solaire d’environ 2 km/s que nous essayons de mesurer. Ce mouvement orbital produit effectivement un décalage Doppler de tout le spectre solaire. Cependant, cet effet s’applique de manière égale à tous les points que nous pouvons mesurer : en d’autres termes, puisque tout le spectre est décalé de manière uniforme, tout s’annule. Il en va de même pour toute vitesse radiale du Soleil par rapport à la Terre (qui varie légèrement tout au long de l’année car l’orbite de la Terre est elliptique).
La formule fondamentale reliant le décalage Doppler à la vitesse est :
Où :
-
\(\Delta\lambda\) est le décalage en longueur d’onde (ce qu’on cherche à mesurer)
-
\(\lambda_0\) est la longueur d’onde au repos de la raie spectrale (typiquement la longueur d’onde H-alpha)
-
\(v\) est la vitesse le long de la ligne de visée
-
\(c\) est la vitesse de la lumière (299 792 km/s)
La méthodologie de mesure
Travaux antérieurs
Je ne suis pas la première personne à essayer de faire cette mesure en spectrohéliographie amateur. En 2017, Peter Zetner a expliqué sur CloudyNights comment mesurer la vitesse différentielle en utilisant un spectrohéliographe. Il a expliqué cette méthodologie en profondeur dans le livre Astronomie solaire - Observer, photographier et étudier le Soleil. Sa méthodologie repose sur des mesures utilisant la raie Na D2. mais peut aussi être appliquée sur d’autres raies brillantes incluant la raie Fe I couramment utilisée à 5250.2 Å, et implique de comparer les intensités des pixels, en les moyennant à différentes latitudes. Les résultats sont meilleurs en effectuant plusieurs scans et en moyennant les données. Bien que cela fonctionne, je voulais essayer une méthodologie différente :
-
Utiliser un seul scan : les images Doppler que JSol’Ex ou INTI peuvent produire sont en général très cohérentes et montrent que toutes les données dont nous avons besoin sont déjà présentes
-
Éviter les intensités de pixels : celles-ci sont très sensibles à l’assombrissement centre-bord, aux conditions d’observation (par exemple les nuages, même fins) ou au vignetage (assombrissement des images le long de la fente)
-
Rendre possible l’utilisation de scans H-alpha, non pas parce qu’ils donneraient une valeur précise de la vitesse du plasma de la photosphère, mais parce que c’est la raie la plus largement imagée dans les observations solaires amateurs
Les résultats, bien sûr, dépendront de la raie observée. La méthodologie que je décris ci-dessous est capable de retourner des résultats raisonnables sur plusieurs raies (H-alpha, Na D2. Fe I) mais échouera complètement sur certaines autres (par exemple Ca II K, typiquement parce que la raie est trop large).
Plongeons-nous dans la méthodologie.
|
Note
|
L’implémentation décrite ici a été développée de manière itérative basée sur des observations réelles. Je ne suis pas physicien solaire, juste un ingénieur essayant d’extraire des données significatives des captures de spectrohéliographe. L’algorithme fonctionne raisonnablement bien en pratique mais devrait être validé par rapport à des mesures professionnelles pour toute application scientifique. C’est pourquoi cette fonctionnalité est annoncée comme expérimentale. |
Comparaison des limbes Est-Ouest
La clé pour comprendre la méthodologie est qu’elle repose sur l’analyse et l’ajustement de profils de raies spectrales. Elle nécessite d’extraire les profils de raies spectrales à différents endroits du disque solaire, de préférence près des limbes où les vitesses sont les plus élevées (plus on s’approche du méridien solaire, plus les vitesses sont faibles et donc difficiles à détecter).
La mesure de rotation différentielle extrait les vitesses de rotation solaire en comparant les décalages Doppler entre les points des limbes Est et Ouest à la même latitude héliographique.

Pour chaque latitude (par exemple, 20° Nord), l’algorithme :
-
Sélectionne un point sur le limbe Est
-
Sélectionne le point correspondant sur le limbe Ouest à la même latitude
-
Mesure la position de la raie spectrale à chaque point
-
Calcule la différence : Ouest - Est
Cette approche différentielle a un avantage crucial : elle annule les erreurs systématiques. Tout décalage instrumental, erreur de calibration en longueur d’onde, ou décalage de référence affecte les deux mesures de manière égale et disparaît quand nous prenons la différence.
Cependant, une seule mesure Est-Ouest à chaque latitude n’est pas assez fiable. Les conditions de seeing, l’activité solaire locale, ou les erreurs d’ajustement peuvent corrompre les mesures individuelles. Pour améliorer la précision, JSol’Ex échantillonne plusieurs longitudes à travers la région du limbe (typiquement 14 points de 62° à 88° de longitude) et agrège ces mesures. Cette redondance permet de rejeter les valeurs aberrantes et fournit une estimation d’erreur basée sur la cohérence des mesures.
La vitesse mesurée est alors :
Le facteur 2 apparaît parce que nous mesurons la différence entre les limbes s’approchant et s’éloignant.
De la vitesse mesurée à la vitesse équatoriale
La vitesse que nous mesurons dépend de la géométrie : quelle fraction de la vitesse de rotation est projetée le long de notre ligne de visée. À l’équateur et au limbe, nous voyons la vitesse de rotation complète. À des latitudes plus élevées ou plus près du centre du disque, nous n’en voyons qu’une fraction.
Le facteur de correction géométrique est :
Où :
-
\(\phi\) est la latitude héliographique
-
\(\theta\) est la longitude héliographique (0° au centre du disque, ±90° aux limbes)
Trouver le centre de la raie spectrale
La partie la plus difficile de la mesure est de déterminer précisément le centre de la raie d’absorption. Un décalage de seulement 0.01 Å correspond à une vitesse d’environ 0.5 km/s, ce qui est significatif par rapport à la vitesse équatoriale typique d’environ 2 km/s.
JSol’Ex utilise l'ajustement de profil de Voigt pour mesurer le centre de la raie. Le profil de Voigt est la convolution d’un profil gaussien et d’un profil lorentzien, qui modélise précisément la forme des raies d’absorption solaires. La composante gaussienne représente l’élargissement Doppler thermique, tandis que la composante lorentzienne représente l’élargissement naturel et de pression.
Pour chaque point de mesure, l’algorithme :
-
Extrait un profil spectral du fichier SER à la position correspondante
-
Ajuste un profil de Voigt à la raie d’absorption
-
Enregistre la position du centre de raie ajustée
Le paramètre configurable "demi-largeur d’ajustement de Voigt" (par défaut : 2 Å) contrôle quelle proportion des ailes de la raie sont incluses dans l’ajustement.
Systèmes de coordonnées
L’un des aspects les plus délicats de cette implémentation est de transformer correctement les coordonnées que nous manipulons. L’algorithme commence avec les coordonnées héliographiques (où nous voulons mesurer) et les transforme en coordonnées des trames SER originales (où les données spectrales se trouvent).
1. Coordonnées héliographiques (point de départ)
Nous commençons par spécifier des points en coordonnées héliographiques :
-
Latitude : -90° (pôle sud) à +90° (pôle nord)
-
Longitude : 0° au centre du disque, ±90° aux limbes
Cela nécessite deux paramètres solaires calculés à partir de la date d’observation :
-
B0 : La latitude héliographique du centre du disque (varie tout au long de l’année)
-
P : L’angle de position de l’axe de rotation (l’inclinaison du Soleil vu depuis la Terre)
2. Coordonnées image
Les coordonnées héliographiques sont converties en positions de pixels dans l’image reconstruite. Cela implique d’inverser les corrections appliquées pendant la reconstruction :
-
Correction de l’angle P
-
Retournement/rotation
-
Distorsion géométrique
-
Angle d’inclinaison
-
Recadrage
3. Coordonnées du fichier SER (destination)
Finalement, les coordonnées image sont mappées vers le fichier vidéo SER brut :
-
Numéro de trame : Position dans la séquence de scan (dérivée de la coordonnée x)
-
Colonne : Position le long de la fente (dérivée de la coordonnée y)
-
Ligne : Direction spectrale (longueur d’onde)
Ce mapping inverse nous permet d’extraire le profil spectral exact à n’importe quelle position héliographique.
Le pipeline de traitement des données
Les mesures brutes sont bruitées. Pour produire une courbe de rotation propre, JSol’Ex utilise un pipeline de traitement en deux étapes :
Étape 1 : Agrégation en longitude
Comme décrit précédemment, à chaque latitude, plusieurs longitudes sont échantillonnées (typiquement 14 points à travers la région du limbe). Ces mesures sont combinées en utilisant l’une des trois méthodes (la médiane par défaut mais vous pouvez choisir) :
-
Médiane : Robuste aux valeurs aberrantes, utilise la valeur centrale
-
Moyenne : Simple moyenne arithmétique
-
Moyenne pondérée : Les points plus proches du limbe (où le signal Doppler est plus fort) ont un poids plus élevé
L’estimation d’erreur de cette étape représente la cohérence des mesures à travers les longitudes.
Étape 2 : Lissage en latitude
Même après l’agrégation en longitude, les mesures latitude par latitude restent bruitées. Les bins de latitude individuels peuvent encore être affectés par des caractéristiques localisées (taches solaires, facules) ou simplement par la dispersion des mesures.
Puisque nous nous attendons à ce que la rotation solaire varie de manière lisse avec la latitude (suivant les termes \(\sin^2\phi\) et \(\sin^4\phi\) de la loi de rotation différentielle), nous pouvons exploiter cette contrainte physique pour réduire davantage le bruit. JSol’Ex applique un filtre de lissage qui combine les points de latitude voisins dans une fenêtre configurable (par défaut : 5°).
De manière importante, les erreurs de l’étape 1 sont propagées plutôt que recalculées à partir de la dispersion dans la fenêtre de lissage. Cela garantit que les barres d’erreur représentent l’incertitude de mesure, pas les variations physiques de latitude.
Pour l’agrégation médiane :
Pour la moyenne :
Le résultat et la comparaison avec la théorie
La forme standard de la loi de rotation différentielle (aussi connue comme la formule de Faye, même si la formule originale n’incluait pas le 3ème terme) est :
Où :
-
\(\phi\) est la latitude héliographique
-
\(A\) est le taux de rotation équatorial
-
\(B\) et \(C\) contrôlent la diminution de la vitesse avec la latitude
JSol’Ex compare les résultats mesurés avec les coefficients largement utilisés de Snodgrass & Ulrich (1990) :
-
\(A = 14.713\) deg/jour (taux de rotation équatorial)
-
\(B = -2.396\) deg/jour
-
\(C = -1.787\) deg/jour
Cela donne une période de rotation équatoriale d’environ 24.5 jours et une période polaire d’environ 34 jours. Convertie en vitesse linéaire à la surface solaire (rayon ≈ 696 000 km), la vitesse de rotation équatoriale est d’environ 2.0 km/s.
JSol’Ex ajuste également ses propres coefficients A, B, C à partir de vos mesures, permettant une comparaison directe avec les valeurs de référence.
Résultats
Ci-dessous des exemples de profils de rotation différentielle mesurés avec JSol’Ex en utilisant deux raies spectrales différentes. Ces mesures ont été prises à des dates différentes avec des conditions de seeing différentes.
Fe I 5883 Å
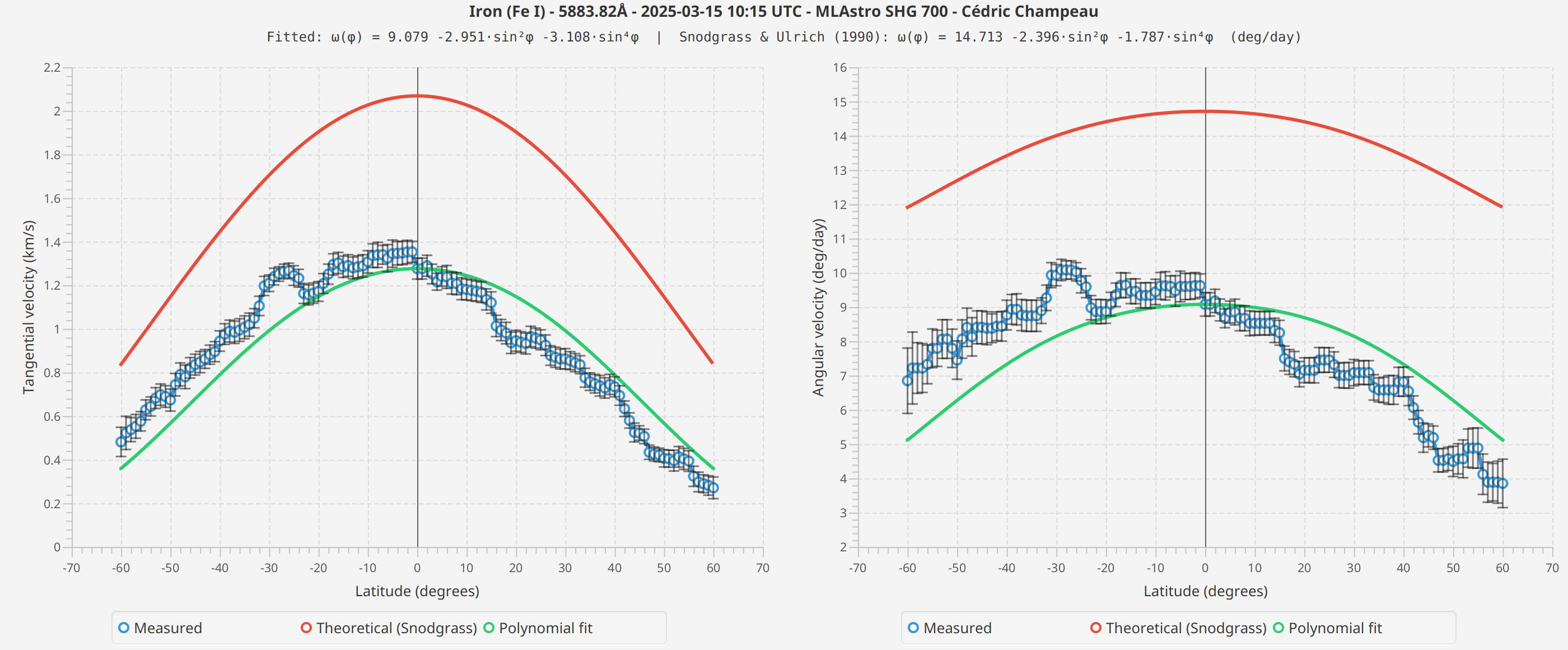
H-alpha
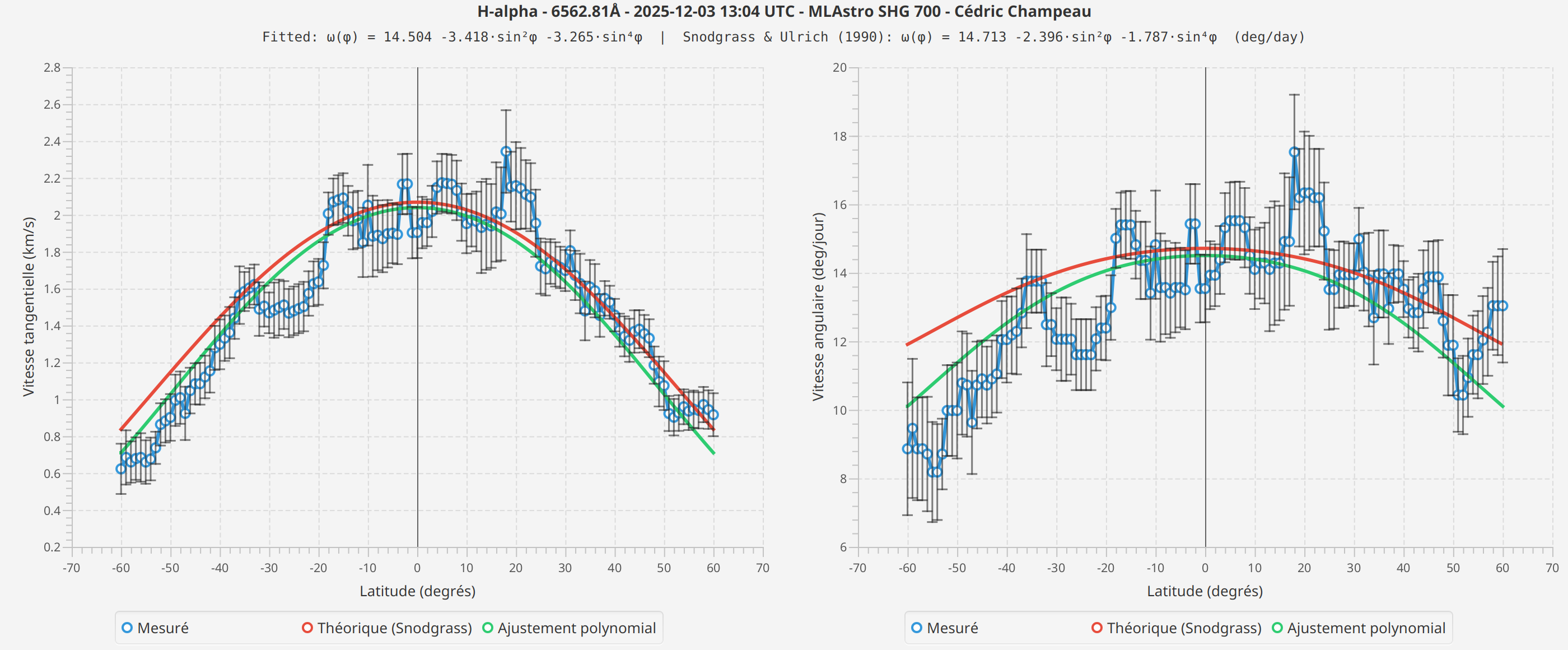
Observations
Les profils mesurés montrent la forme générale attendue : des vitesses plus élevées à l’équateur, diminuant vers les pôles. Les courbes ajustées suivent raisonnablement bien le profil théorique de Snodgrass.
Cependant, j’observe des différences entre les raies spectrales que je ne peux pas entièrement expliquer. Les mesures Fe I montrent des vitesses absolues différentes de H-alpha, et les coefficients ajustés diffèrent entre les scans.
Plusieurs facteurs pourraient contribuer à ces différences :
-
Hauteur de formation : Différentes raies spectrales se forment à différentes hauteurs dans l’atmosphère solaire, et les taux de rotation peuvent varier avec l’altitude (comme suggéré par des recherches récentes de la mission CHASE)
-
Conditions de seeing : Les scans ont été pris à des dates différentes avec des conditions atmosphériques différentes
-
Différences de profil de raie : H-alpha et Fe I ont des largeurs et profondeurs de raie différentes, ce qui peut affecter la précision de l’ajustement de Voigt
-
Effets systématiques : Il peut y avoir des facteurs instrumentaux ou algorithmiques que je n’ai pas identifiés
Je présente ces résultats tels qu’ils sont, sans essayer de tirer des conclusions sur quelle mesure est "correcte" ou ce qui cause les différences observées. Plus de mesures sur différentes dates, raies spectrales et instruments seraient nécessaires pour comprendre ces variations.
Mesurer en pratique
La qualité des résultats dépend fortement du seeing atmosphérique. Un mauvais seeing floute les raies spectrales et rend la détermination précise du centre difficile. Les meilleurs résultats sont obtenus avec d’excellentes conditions de seeing et un instrument bien focalisé. Enfin et surtout, une haute résolution spectrale est préférée, ce qui est normalement le cas avec le Sol’Ex (HR) ou le SHG 700.
Vous pouvez aussi vous demander quelle raie spectrale vous devriez observer. J’ai testé l’algorithme avec Fe I, Na D2 et H-alpha, donnant les résultats ci-dessous. En pratique, les raies d’absorption fortes devraient en théorie produire les meilleurs résultats, car :
-
La profondeur de raie devrait être suffisante pour un ajustement précis
-
Les ailes devraient être bien définies pour l’ajustement de Voigt
-
Le rapport signal sur bruit devrait être élevé
Les raies très larges comme Ca II K sont trop larges pour un ajustement de Voigt précis et produiront des résultats peu fiables. Les raies trop étroites peuvent aussi représenter un défi pour l’ajustement de Voigt mais peuvent fonctionner aussi.
L’impact de la détection de la raie spectrale
Un facteur subtil mais important affectant la précision absolue des mesures est la correction polynomiale utilisée pendant la reconstruction d’image. Comprendre ceci est essentiel pour interpréter correctement vos résultats.
Pendant le traitement du spectrohéliographe, JSol’Ex calcule un polynôme qui fait correspondre chaque position de colonne le long de la fente vers la position de ligne attendue du centre de la raie spectrale. Ce polynôme est calculé à partir de la moyenne des trames SER dans le scan (une heuristique est utilisée pour inclure les trames contenant des données solaires réelles, pas le fond de ciel).
Une telle détection est cruciale car la raie spectrale n’est pas droite à travers la fente en raison de phénomènes optiques : elle constitue ce que nous appelons souvent le "smile". Par conséquent, le centre de raie peut être à la ligne 300 à la colonne 500. mais à la ligne 350 à la colonne 1000. Le polynôme capture cette courbure.
En mesurant les positions de raie relativement au polynôme, nous éliminons efficacement la distorsion optique de nos mesures. Sans cette référence, nous mesurerions la somme de la courbure optique plus le décalage Doppler, rendant impossible l’extraction des minuscules signaux de vitesse que nous recherchons.
Une question clé est : pourquoi ne pouvons-nous pas simplement mesurer la position absolue de la raie spectrale dans chaque trame et calculer les vitesses directement ?
La réponse réside dans la précision requise. Une vitesse de 2 km/s correspond à un décalage de longueur d’onde de seulement ~0.04 Å à H-alpha. Avec une dispersion spectrale typique de 0.1-0.2 Å/pixel, c’est un décalage de seulement 0.2 à 0.4 pixels.
La courbure optique à travers la fente, d’autre part, peut facilement s’étendre sur 10-30 pixels ou plus. Toute tentative de mesurer les positions absolues de raie serait complètement dominée par cette courbure, rendant la détection Doppler impossible.
Le polynôme sert de référence de base. En mesurant comment la position de raie dans chaque trame individuelle dévie du polynôme, nous isolons la composante Doppler de la composante optique. C’est l’idée clé qui rend les mesures de précision sub-pixellaire possibles, avec l’ajustement de Voigt.
Un mot sur les images Doppler
Ceci, d’ailleurs, est aussi une raison pour laquelle les images Doppler sont différentes quand on scanne en AD vs DEC. Parce que c’est une question souvent posée, et qu’il m’a fallu des mois pour comprendre la raison, je pense qu’il vaut la peine de passer un peu de temps à expliquer le phénomène. Je dois cette explication à Jean-François Pittet et Christian Buil, d’une discussion il y a quelques semaines sur la mailing list Sol’Ex.
Scan en AD vs scan en DEC : une différence critique pour les images Doppler
Les spectrohéliographes peuvent scanner le Soleil dans deux directions :
-
Scan en AD (Ascension Droite) : La fente est orientée Nord-Sud, et le scan procède Est-Ouest
-
Scan en DEC (Déclinaison) : La fente est orientée Est-Ouest, et le scan procède Nord-Sud
Ce choix a des implications profondes pour la visibilité Doppler, comme expliqué par Jean-François Pittet sur la mailing list Sol’Ex.
Scan en AD : Doppler visible dans les images
En mode scan AD, chaque trame capture une tranche verticale du Soleil du pôle Nord au pôle Sud. Au cours du scan :
-
Les premières trames capturent le limbe Est (s’approchant, décalé vers le bleu)
-
Les trames du milieu capturent le centre du disque (pas de vitesse radiale)
-
Les dernières trames capturent le limbe Ouest (s’éloignant, décalé vers le rouge)
Quand JSol’Ex calcule le polynôme à partir de la moyenne de toutes les trames, les contributions Est et Ouest s’équilibrent. Le blueshift du limbe Est est annulé par le redshift du limbe Ouest. Le polynôme résultant représente la référence "neutre" : approximativement la position de raie au centre du disque sans décalage Doppler.
En conséquence, quand nous reconstruisons l’image au décalage de pixel 0. les décalages Doppler deviennent visibles comme différences de contraste :
-
Le limbe Est apparaît plus sombre (raie décalée dans la bande passante)
-
Le limbe Ouest apparaît plus clair (raie décalée hors de la bande passante)
C’est pourquoi les images Doppler des scans AD montrent l’asymétrie caractéristique Est-Ouest.
Scan en DEC : Doppler "absorbé" par le polynôme
En mode scan DEC, chaque trame capture une tranche horizontale du Soleil d’Est en Ouest. Voici la différence critique : tous les pixels dans une seule trame voient approximativement le même décalage Doppler.
Par exemple, si la trame actuelle capture la moitié Est du disque :
-
Tous les points dans cette trame s’approchent de nous
-
Tous les points ont un blueshift similaire
Quand JSol’Ex calcule le polynôme à partir de la moyenne de toutes les trames, il ne capture pas seulement la courbure optique : il capture aussi le décalage Doppler moyen à travers le scan. Mais voici le problème : le décalage Doppler varie systématiquement à travers le scan (les trames Est sont décalées vers le bleu, les trames Ouest sont décalées vers le rouge).
Le polynôme "absorbe" effectivement une moyenne pondérée de ces décalages Doppler. Quand nous mesurons ensuite les positions de raie relativement à ce polynôme, une grande partie du signal Doppler a déjà été soustraite. Les images Doppler résultantes ne montreront plus la rotation du soleil (ce qui peut aussi être un avantage, pour d’autres types d’observations).
C’est pourquoi les spectrohéliographes expérimentés préfèrent souvent le scan AD pour le travail Doppler : le signal Doppler est plus visible et plus facile à détecter.
La complication de l’angle P
Il y a une subtilité supplémentaire : l’axe de rotation du Soleil n’est pas perpendiculaire à l’écliptique. L'angle P (angle de position de l’axe de rotation) varie tout au long de l’année d’environ -26° à +26°.
Deux fois par an (vers début juin et début décembre) l’angle P est proche de zéro. À ces moments :
-
Le scan AD est vraiment parallèle à l’équateur solaire
-
Le motif Doppler Est-Ouest s’aligne parfaitement avec la direction de scan
À d’autres moments, quand P est non nul :
-
L’axe de rotation est incliné par rapport à la direction de scan
-
Le motif Doppler est tourné par rapport aux axes de l’image
-
Une partie du signal Doppler "fuit" dans la moyenne polynomiale même en mode AD
C’est une des raisons pour lesquelles les mesures de rotation différentielle peuvent montrer des résultats légèrement différents à différentes périodes de l’année, bien que nous prenions en compte les angles P et B0.
Implications pour les mesures de rotation différentielle
Ceci explique pourquoi le scan AD est essentiel pour les mesures de vitesse différentielle :
En mode AD, les points des limbes Est et Ouest à la même latitude correspondent à la même colonne sur la fente (même position de fente, trames différentes).
La valeur du polynôme à cette colonne est calculée à partir de la moyenne de toutes les trames (limbe Est, centre du disque, et limbe Ouest) donc les décalages Doppler s’annulent dans la moyenne.
Quand nous calculons (Ouest - polynôme) - (Est - polynôme), les termes du polynôme sont identiques et s’annulent, nous laissant avec la vraie différence Doppler Ouest - Est.
En mode DEC, les points des limbes Est et Ouest à la même latitude correspondent aux extrémités opposées de la fente (colonnes différentes, même trame). Le polynôme à la colonne Est est calculé à partir de trames qui voient toutes le limbe Est à cette position, donc le polynôme absorbe le blueshift. De même, le polynôme à la colonne Ouest absorbe le redshift. Quand nous calculons la différence, ces décalages Doppler absorbés ne s’annulent pas : ils se soustraient de notre mesure, réduisant significativement le signal mesuré.
C’est pourquoi, en pratique, les scans DEC ne produisent pas d’images Doppler utilisables ou de mesures de vitesse différentielle fiables.
Conseils de configuration
-
Longitude du limbe (par défaut 75°) : Les mesures plus proches du limbe donnent des signaux Doppler plus forts mais risquent des effets d’assombrissement centre-bord
-
Pas de latitude (par défaut 2°) : Des valeurs plus petites donnent une résolution plus fine mais des temps de traitement plus longs
-
Fenêtre de lissage : Devrait être au moins 2× le pas de latitude pour un lissage efficace
Conclusion
Mesurer la rotation différentielle avec du matériel amateur aurait semblé impossible il y a quelques années seulement. Des pionniers comme Peter Zetner ou Christian Buil nous ont montré la voie. Ce que j’essaie de faire, comme toujours avec JSol’Ex, c’est de rendre ceci accessible à encore plus de personnes au prix de la "magie", c’est-à-dire que certaines personnes partageront très probablement des résultats sans comprendre la science derrière. Je ne suis pas trop inquiet par cela, parce que je suis moi-même passé par là : apprécier la reconstruction d’images SHG, puis comprendre comment ça fonctionne, puis me poser des questions comme "pourquoi est-il même possible de mesurer des vitesses Doppler si petites ?" : c’est une construction intellectuelle qui prend du temps. Nous, membres de la communauté Sol’Ex, pouvons faire mieux, je pense, pour apporter cela aux masses, en partageant nos idées et en écrivant des logiciels comme celui-ci.
Cette fonctionnalité rejoint la liste croissante des capacités scientifiques dans JSol’Ex : détection des bombes d’Ellerman, identification des régions actives, et maintenant mesure de la rotation différentielle. Chacune de celles-ci met des analyses de niveau professionnel à la portée des astronomes amateurs, mais, comme toujours, soyez prudent avec ce que je dis : je ne suis pas un scientifique, juste un ingénieur. Je n’ai aucun doute que j’ai fait des approximations, ou pris des libertés que je n’aurais probablement pas dû prendre.
Bibliographie
Articles scientifiques
-
Howard, R. & Harvey, J. (1970) - Spectroscopic determinations of solar rotation. Sol Phys 12. 23-51
-
Snodgrass, H.B. (1984) - Separation of large-scale photospheric Doppler patterns. Sol Phys 94, 13-31
-
Beck, J.G. (2000) - A comparison of differential rotation measurements. Sol Phys 191, 47-70
-
Corbard, T. et al. (2025) - Rotational radial shear in the low solar photosphere. A&A 702. A93
